 Mahout 0.10.x is coming. It is a new generation of Mahout that entirely re-thinks philosophy of previous Mahout line of releases.
Mahout 0.10.x is coming. It is a new generation of Mahout that entirely re-thinks philosophy of previous Mahout line of releases.
First, and foremost, to state the obvious, Mahout abandons MapReduce based algorithms. We still support them (and they are now moved to mahout-mr artifact). But we do not create any new ones.
Second, we shift the focus from being a collection of things to being a programming environment, as it stands, for Scala.
Third, we support different distributed engines, aka "backs". As it stands, we run on Spark and H20, but hope to add Apache Flink translation as well, provided we get help there.
Many people are coming with obvious question: so how it is different from stuff like MLLib? Here, I'll try to emphasize key philosophical points of this work.
1. We want to help people to create their own math, as opposed to just taking and plugging in an off-the-shelf black-box solution.
Indeed, having a fairly well-adjusted and complicated black box solutions is a good thing. People spent quite a bit of time researching and optimizing them.
Problem is, very often off-the-shelf is just not enough. We want to customize and build our own models, our own features, our own specific rules and ensembles. And we want to do it quickly and try it now.
Let's look at some intentionally simple examples. Suppose we want to compute a column-wise variances on a matrix. For that we are going to use simple formula
\[
\mathrm{var}\left(x\right)=\mathbb{E}\left(x^{2}\right)-\left[\mathbb{E}\left(x\right)\right]^{2}
\]
applied column-wise on our big, distributed matrix $\mathbf{X}$. Here is how it is going to look in new Mahout enviornment:
val mu = X colMeans
val variance = (X * X colMeans) -= mu * mu
That's it. All in fully distributed fashion. On Spark or H20.
Let's take on a little bit more complicated case. What if we want to compute n-dimensional column-wise covariance matrix of the dataset X?
Assuming that
\[
\boldsymbol{x}_{i}\triangleq\mathbf{X}_{i*},
\]
i.e. every row is a point in the dataset, we can use multivariate generalization of the previous formula:
\[\mathrm{cov}\left(\mathbf{X}\right)=\mathbb{E}\left(\boldsymbol{xx}^{\top}\right)-\boldsymbol{\mu\mu}^{\top},\]
where
\[\boldsymbol{\mu}=\mathbb{E}\left(\boldsymbol{x}\right).\]
Here is the Mahout code for that formula:
val mu = X.colMeans()
val mxCov = (X.t %*% X).collect /= X.nrow -= (mu cross mu)
This code is actually a so called "thin" procedure, i.e. the one that assumes that while the $m\times n$ input matrix $\mathbf{X}$ is too big to be an in-core matrix, the $n\times n$ covariance matrix will fit into memory in one chunk. In other words, it assumes $n\ll m$. The code for "wide" distributed covariance computation needs couple more lines but is just as readable.
So, what is the difference between Mahout 0.10.x and MLLib? Well, what is the difference between R package and R? What is the difference between libsvm and Julia? What is difference between Weka and Python? And how to think about it -- R for Spark? Hive for math? Choose your poison.
Bottom line, we want to help you create your own math at scale. (And hopefully, come back to us and share it with us).
2. We want to simplify dialect learning. We actually build the environment in image of R. Initially, we also had DSL dialect (enabled via separate import) for Matlab, but unfortunately Scala operator limits do not make it possible to implement entire Matlab operator set verbatim, so this work received much less attention, and instead, we focused on R side of things.
What it means is it should be easily readable by R programmers. E.g. A %*% B is matrix multiplication,
A * B is elementwise Hadamard product, methods like colMeans, colSums are following R naming for those.
Among other things, arguably,
math written in R-like fashion is easier to understand and maintain than the same things written in other basic procedural or functional environments.
3. Environment is backend-agnostic. Indeed, Mahout is not positioning itself as Spark-specific. You can think of it that way if you use Spark, but if you use H20, you could think of it as H2o-specifc (or, hopefully, "Apache Flink-specifc" in the future) just as easily.
All the examples above are not containing a single Spark (or h20) imported dependency. They are written once but run on any of supported backs.
Not all things can be written with the subset of back-independent techniques of course, more on that below. But quite a few can -- and the majority can leverage at least some as the backbone. E.g. imagine that dataset $\mathbf{X}$ above is result of embarrassingly parallel statistical Monte Carlo technique (which is also backend-independent). And just like that we perhaps get a backend-agnostic Gibbs sampler.
4. "Vs. mllib" is a false dilemma. Mahout is not taking away any capabilities of the backend. Instead, one can think of it as an "add-on" over e.g. Spark and all its technologies. (same for h2o).
Indeed, it is quite common to expect that just Algebra and stats are not enough to make the ends meet. In Spark's case, one can embed algebraic pipelines by importing Spark-specific capabilities. Import MLLib and all the goodies are here. Import GraphX and all the goodies are here as well. Import DataFrame(or SchemaRDD) and use language-integrated QL. And so on.
I personally use one mllib method as a part of my program along with Mahout algebra. On the same Spark context session as the Mahout Algebra session. No problem here at all.
5. Mahout environment is more than just a Scala DSL. Behind the scenes, there is an algebraic optimizer that creates logical and physical execution plans, just like in a database.
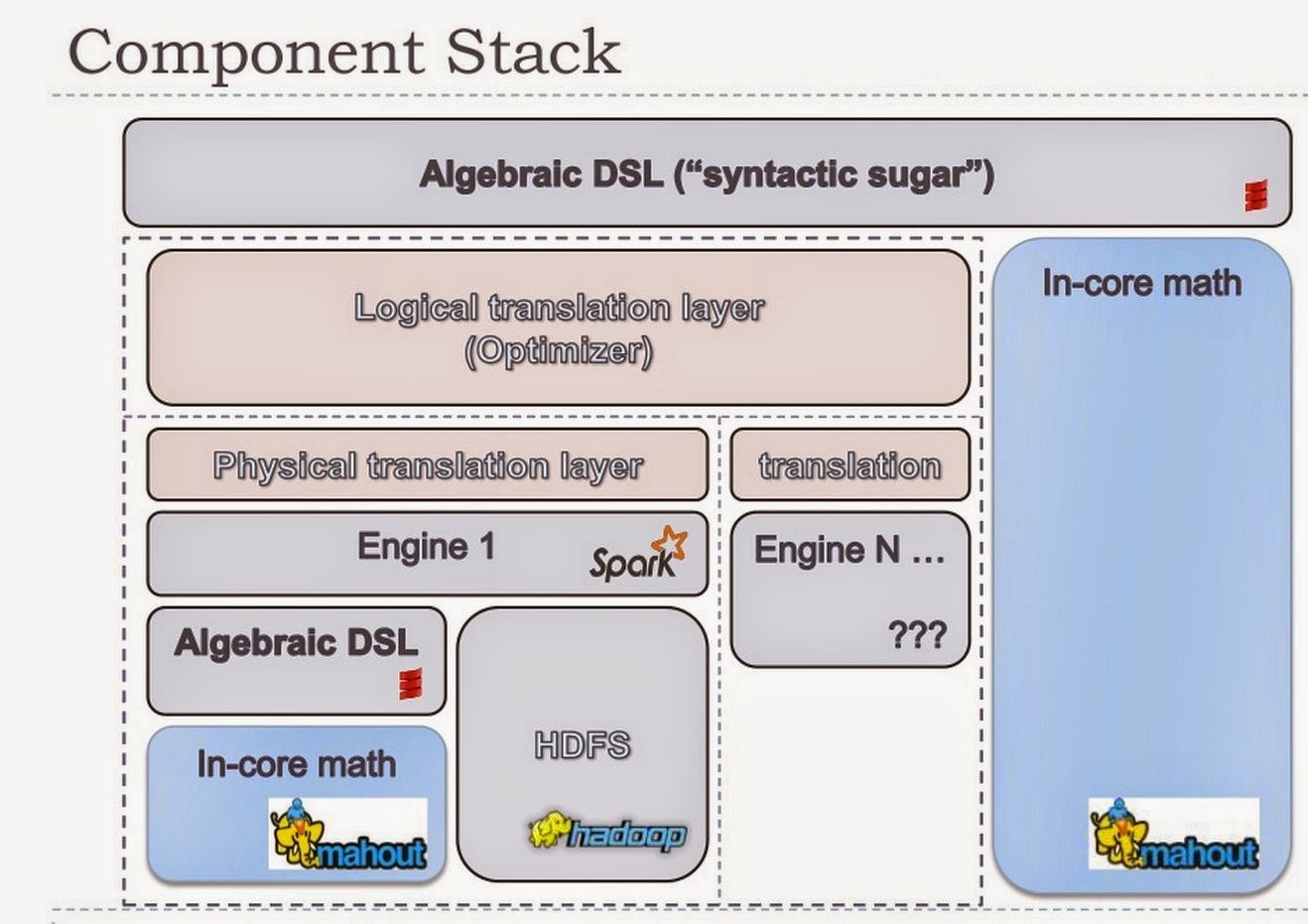 |
| Algebraic Optimizer Stack |
For example, we can understand that a thing like
dlog(X * X + 1).t %*% dlog(X * X + 1)
is in fact (in simplified physical operator pseudo code)
self_square(X.map(x => log(x * x + 1)).
6. Off-the-shelf methods. Of course we want to provide off-the-shelf experience too. Logical thing here is to go with stuff that complements, but not repeats other off-the-shelf things available. Refer to the Mahout site what's in and what's in progress.
But even use of off-the-shelf methods should be easily composable via programming environment and scripting.
Future plans. Work is by no means complete. In fact, it probably just started.
In more or less near future we plan to extend statistical side of things of the environment quite a bit.
We plan to work on performance issues, especially for in-core performance of the algebraic API.
We want to port most of MR stuff to run in the new environment, preferably in a completely backend-agnostic way (and where it is not plausible, we would isolate and add strategies for individual backs for the pieces that are not agnostic).
We plan to add some must-have off-the-shelf techniques such as hyperparameter search.
And of course, there are always bugs and bug fixes.
Longer term, we think it'd be awesome to add some visualization techniques similar to ggplot2 in R, but we don't have capacity to develop anything similar from the ground up, and we are not yet sure what might be integrated in easily and which also works well with JVM based code. Any ideas are appreciated.




